Resolving Shadow Admins: Achieving Maximum Impact with Minimal Effort

Shadow Admins are non-administrative users that hold sensitive privileges which effectively grant them admin-level rights. Such privileges can include direct access to resources or the ability to modify other users’ settings (for example, resetting passwords, gaining “Write All properties” permissions, etc.). In this blog post, we’ll focus on the second type.

There are several reasons why shadow admin accounts are created: human error, mismanagement, a temporary need, or by an attacker who has managed to gain access and wants to hide their presence.

Shadow admins are a known risk for almost every Identity Provider (IdP), including Microsoft Active Directory (AD), Microsoft Entra ID (formerly Azure AD), and Okta, among others. Here, we will discuss shadow admins within AD.

Identity teams continuously search for shadow admin accounts in order to revoke their admin privileges. But this process is often lengthy and tedious, especially if an organization has a large number of shadow admins. My team and I were curious about the common permission configurations that could cause a user to become a shadow admin, as well as the best ways to identify and mitigate them.
In this blogpost, we’ll use algorithmic tools and graph theory to present a novel method to reveal shadow admins within an organization, analyze them, and resolve them.

Understanding the Threat of Shadow Admins

A user account becomes a shadow admin if it has strong privileges over an existing admin account. Similarly, any other account with strong privileges over the shadow admin’s, also becomes a shadow admin.

For example, if Alice had a regular account with admin permissions, she would be a shadow admin. If Bob gained strong permissions over Alice’s, he would also become a shadow admin.

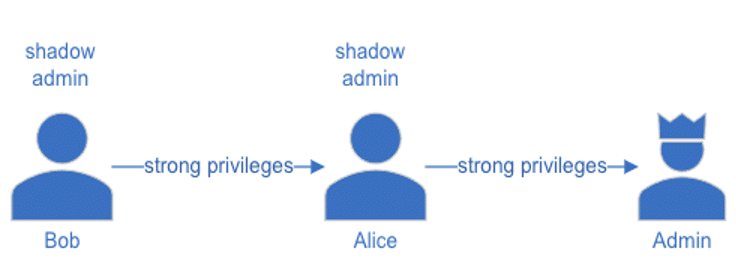
This chain of permissions causes a lot of complications, and reality shows that many shadow admins actually have more than one way to make themselves admins. What makes shadow admin accounts both challenging and risky is that they are not monitored or supervised, and their activity can potentially go undetected.

Interested in learning more about shadow admins and how they threaten your organization? Read this blog post: https://www.silverfort.com/blog/the-hidden-dangers-of-shadow-admins/

So, to resolve the risk of shadow admins we need to revoke some of their excessive permissions, which takes time and effort. Therefore, it makes sense that any organization with many shadow admins would aim to resolve the maximum number of shadow admins with the least amount of effort (i.e., organizational permissions changes).

To do this efficiently, we can retrieve information regarding the permissions of users and groups in a selected set of modification permissions and monitor them. Using logs, we are then able to construct chains of permissions and get details on the shadow admins in the organization.

Translating the Issue

In any organization with shadow admins, there are multiple permission chains that create a connective path between users and the administrative accounts they could potentially take over.

The goal we’ve set for the organization is to make as few changes to permissions as possible, while resolving a large portion of its shadow admins. The question, therefore, is: what permissions are those?

So, let’s rephrase the problem: Identify the optimal set of K permissions that, if revoked, would mitigate the maximum number of shadow admins.

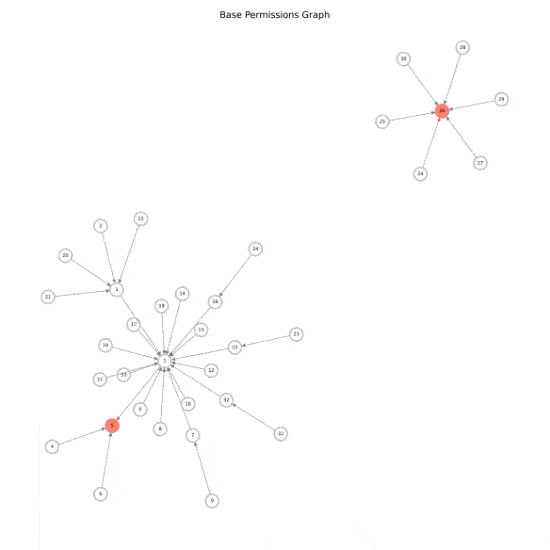
Now that we have this definition, we can convert the problem to a visual one using graph theory. We do this by representing every account or group as a node in a graph and every permission as a directed edge between these nodes. This enables all our permission chains to be displayed and connected on a single graph along with their respective privileges and attributes.

Using the information contained in the permission chains, we can identify who the organizations’ admins and administrative groups are, and mark those in our graph, as they are the end goal of a shadow admin.

At this stage, such a graph would look like this:

Next, we will rewrite the problem statement one more time: Find the set of K edges that, upon removal, would disconnect as many shadow admins as possible from the rest of the graph (i.e., mitigate them).

Breaking Apart the Approach

At first glance, we see a Directed Acyclic Graph (DAG) that represents a network connecting our various permission chains. But let’s think about the representation of the graph and connections, as well as how each entity can hold permission over another. In a way, we can imagine a shadow admin “moving” in our graph from one node to another on its edges. Perhaps even more than one single shadow admin could be capable of such movement.

Now let’s imagine that all shadow admins in the organization start moving towards our red nodes (the admins), then on each path a certain number of shadow admins are “flowing” towards their end goal.

Let’s also note that it doesn’t matter if multiple shadow admins are flowing towards a single node on their path or that the node is a single account. This is because once all shadow admins reach that point only a single account can continue the path.

This, by the way, is reminiscent of the famous “Flow Problem,” a scenario in fluid dynamics where we have a system in which liquid runs through pipes from a few source nodes to a few destination nodes.

So, let’s now turn our eyes to a theorem called “Minimum Cut–Maximal Flow.” This states that the maximum amount of flow in a system passing from the source nodes to the destination nodes is equal to the total weight of the edges in a minimal cut.

We’ll define the following:

• Flow capacity of an edge — for every edge there is an upper limit to the flow passing through it.
• Conservation of flow — incoming flow to a node must be equal to the outgoing flow.
• Cut — the partition of nodes such that it splits the network into two parts:
  • a cut cannot contain both the source and the sink nodes.
  • the weight of a cut is equal to the sum of capacity of outgoing edges.

The algorithm’s goal is to find the maximum flow in a network from a source node to a sink node while minimizing the capacity of the cut separating them. The algorithm iteratively augments the flow along paths from the source to the sink until no more augmenting paths can be found.

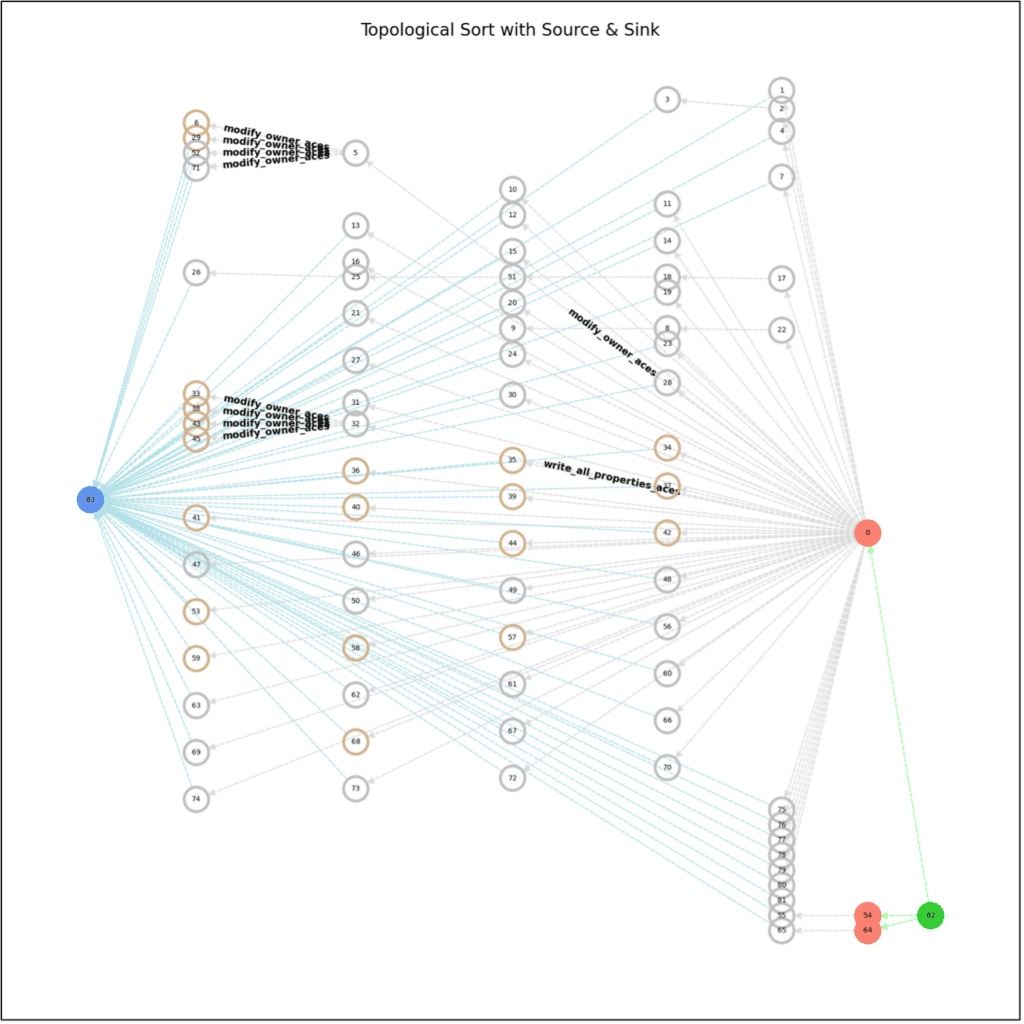
Solving the Flow Problem using this theorem gives us a minimal-cut solution that is equivalent to identifying the set of K edges to remove — since the duality problem is the maximal flow possible through the system, meaning that we are finding a cut that minimizes the weight of the cut while maximizing the partition. The resulting graph where the algorithm will be applied will look something like this:

   

Results and Conclusions

Applying our method to a group of more than 30 organizations, we discovered that the median was around 30 active accounts per organization identified as shadow admins, with a few organizations having as many as 1,000 such accounts.

Applying the algorithm resulted in a minimal cut of a set of edges that, if removed, would mitigate most shadow admins with minimal changes to the organization’s permissions.

The results look like this:

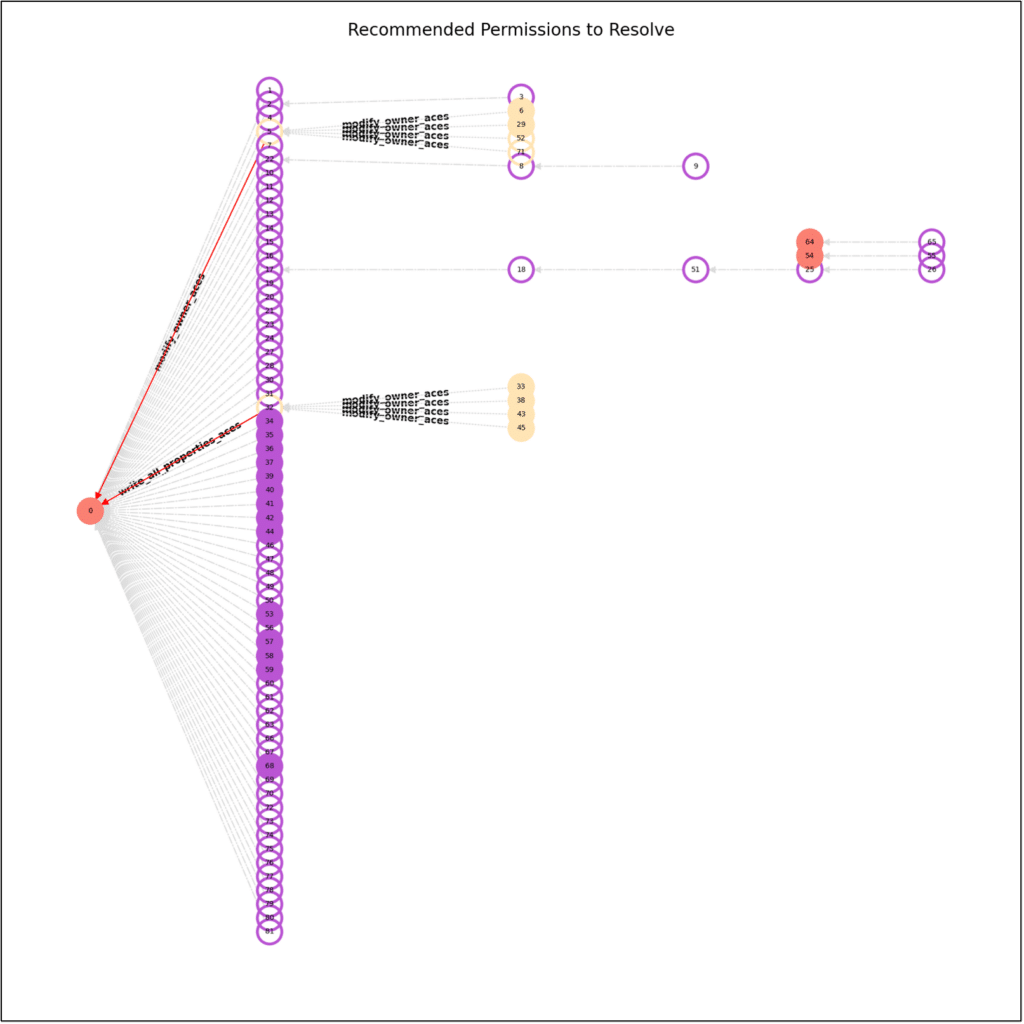
On average, we managed to resolve around 70% of an organization’s shadow admins with a single iteration of the algorithm. Furthermore, all that was needed to achieve that was the revoking of three permissions on average!

This means that we can provide the exact set of edges (i.e., permissions) that the organization should consider revoking that would net the best mitigation of shadow admins with minimal effort.

Closing Thoughts

Shadow admins are a serious threat that is often overlooked, and one not easily mitigated by traditional methods. Having a chain of privileges that leads to a domain admin isn’t always well documented.

One of the common patterns we noticed was that, in reality, there are multiple ways for a user to become a shadow admin. A different approach was much simpler to implement, but it couldn’t tackle such patterns and returned sub-optimal results.

Our solution monitors the permissions given in an IdP environment and can dynamically build the best set of privileges to resolve in order to reduce the number of shadow admins with minimal action.

A method like this can help pinpoint the set of optimal permissions to be resolved with minimal effort, taking a real problem from the cybersecurity domain and visualizing it by utilizing a known algorithm to reach a solution.